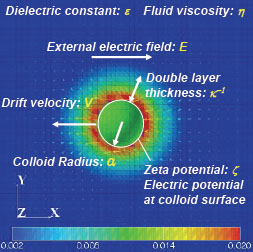
Electrophoresis †

↑

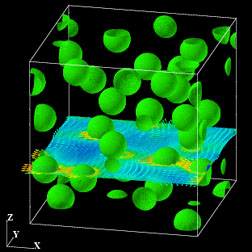
Binary (+/-) charged colloidal particles in aqueous solution (water/counter-ions/salts) under constant electric field. †

  • Simultaneous simulation of 5,000 positive colloids (yellow particles), 5,000 negative colloids (red particles), densities of positive and negative ions (not shown), and solvent flow (not shown). Many-body electrostatic and hydrodynamic interactions are fully taken into account.
Electric field --->
00.jpg time >> 40.jpg
  • Still computing... Please wait.
  • Simulation parameters
    • CFD Lattice: 256 x 256 x 256 mesh
    • Number of Particles: N = 10,000 (5,000(+) and 5,000(-))
    • Diameter of Particles: D = 6 mesh
    • Volume Fraction: Φ = 0.06...
    • Number of Iteration Steps: 40,000
    • Computation Time: 5 Days on Intel Core-i7-3.2GHz (with ICC+MKL+OMP)
↑

Electrophoresis of a single colloidal particle †

  • Simulation parameters
    • CFD Lattice: 64 x 64 x 64 mesh
    • Number of Particles: N = 1
    • Diameter of Particles: D = 10 mesh
    • Particles Reynolds No.: Re ~ 1
    • Number of Iteration Steps: 5,000
↑

Electrophoresis of 32 colloidal particles †

  • Simulation parameters
    • CFD Lattice: 64 x 64 x 64 mesh
    • Number of Particles: N = 32
    • Diameter of Particles: D = 10 mesh
    • Volume Fraction: Φ = 0.025
    • Particles Reynolds No.: Re ~ 1
    • Number of Iteration Steps: 5,000
↑

Electrophoresis of 32 positive and 32 negative colloidal particles †

  • Simulation parameters
    • CFD Lattice: 64 x 64 x 64 mesh
    • Number of Particles: N = 64
    • Diameter of Particles: D = 10 mesh
    • Volume Fraction: Φ = 0.05
    • Particles Reynolds No.: Re ~ 1
    • Number of Iteration Steps: 5,000
  • Related papers
    • K. Kim, Y. Nakayama, R. Yamamoto, Direct Numerical Simulations of Electrophoresis of Charged Colloids
      Physical Review Letters Vol.96, 208306 (2006).
      • filesample1.udf reproduces the second data from the left in Fig. 1(b).
        ( V = 0.1234 -> Em=3e*eta*V/2*epsilon*kBT*E=0.9255..)
      • filesample2.udf reproduces the third green data from the left in Fig. 3(b)

single.jpg z100_32particles_random.jpg

Electrophoresis of small particles are of great importance not only in pure science, but also in several engineering fields. Analytical theories have been well established for dilute dispersions, but not for dense dispersions because of the difficulties ascribable to the hydrodynamic and electrostatic many-body effects. Therefore electrophoresis of dense colloidal dispersions has been an important unsolved problem for more than a decade. Computer simulation is a promising tool to solve this problem, however, simulations performed so far for electrophoresis of charged colloids remain either for small number of particles with some quantitative reliability or for many particles with less reliability. The main difficulty is how to resolve the hydrodynamic and electrostatic interactions acting on colloidal particles consistently within a reasonable computation time.

In this study, we examined the volume fraction dependency of the electrophoretic mobility using a unique simulation scheme, called the smoothed profile method (SPM) , and found that it clearly deviates from the mean field type theories based on the cell model when overlapping of the electric double layer becomes important. Here, the many body electro-hydrodynamic interactions are fully taken into account through the diffuse interface between colloids and fluids. Then the time evolutions of colloidal particles, ions, and host fluids are computed simultaneously by solving the Newton's, the Navier--Stokes, and the advection-diffusion equations. The present study is the first successful attempt which provides quantitative data necessary to examine the reliability of several analytic models proposed for electrophoresis of dense colloidal dispersions.